Як рахувати подвійну суму?
Розберемось на прикладі:
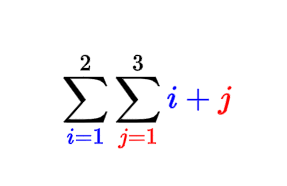
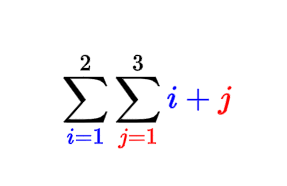
- суму зліва ми назвемо зовнішньою,
- суму з права - внутрішньою
Щоб порахувати подвійну суму потрібно розуміти Знак суми
КРОК 1: рахуємо внутрішню суму як завжди, тут j змінна, i просто стала (константа).
Знак зовнішньої суми залишаємо:
\begin{equation}
\begin{split}
\sum_{\color{blue}{i=1}}^{2} \sum_{\color{red}{j=1}} ^{3}{ \color{blue}{i}+\color{red}{j}} &=
\sum_{\color{blue}{i=1}}^{2}(\color{blue}{i}+\color{red}{1})+\\&+
(\color{blue}{i}+\color{red}{2})+\\&+(\color{blue}{i}+\color{red}{3})=\\ змінюється \\тільки \hspace{0.4em} \color{red}{j}\hspace{0.4em} \\
& =\sum_{\color{blue}{i=1}}^{2} (3\cdot \color{blue}{i}+\color{red}{6})
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\sum_{\color{blue}{i=1}}^{2} \sum_{\color{red}{j=1}} ^{3}{ \color{blue}{i}+\color{red}{j}} &=
\sum_{\color{blue}{i=1}}^{2}(\color{blue}{i}+\color{red}{1})+(\color{blue}{i}+\color{red}{2})+(\color{blue}{i}+\color{red}{3})=\\
\ змінюється\hspace{0.4em} тільки \hspace{0.4em} \color{red}{j},\\ \hspace{0.4em}
\color{blue} i \hspace{0.4em}просто\hspace{0.4em} стала\\
& =\sum_{\color{blue}{i=1}}^{2} (3\cdot \color{blue}{i}+\color{red}{6})
\end{split}
\end{equation}
КРОК 2: Потім рахуємо зовнішню суму як завжди, міняється i
\begin{equation}
\begin{split}
&\sum_{\color{blue}{i=1}}^{2} (3\cdot \color{blue}{i}+6)=\\&=(3\cdot \color{blue}{1}+6)+\\&+(3\cdot \color{blue}{2}+6)=\\&
=9+12=21
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\sum_{\color{blue}{i=1}}^{2} (3\cdot \color{blue}{i}+6)&=(3\cdot \color{blue}{1}+6)+(3\cdot \color{blue}{2}+6)=\\&
=9+12=21
\end{split}
\end{equation}
Тепер попробуйте порахувати наступний приклад самі!
Рішення можете перевірити в низу сторінки.
Приклад 1
(для практики ):
\begin{equation}
\begin{split}
\sum_{{i=1}}^{4}\sum_{{j=1}}^{2} i+j=?
\end{split}
\end{equation}
Часта помилка при рахуванні суми:
$\sum_{{i=1}}^{2}
( \color{blue}{i}+i)\neq 1+2$
має бути
$\sum_{{i=1}}^{2}
( \color{blue}{i}+i)=(1+1)+\\ \hspace{5em}+(2+2)$
Тобто спочатку ми підставляємо 1 в обидві "i", потім так само 2 і додаємо.
Чи рівносильно:
$\sum_{{i=1}}^{2}
( \color{blue}{i}+i)=\sum_{{i=1}}^{2} \color{blue}{2\cdot i}\\
\hspace{5em}=2\cdot 1+2\cdot 2$
Давайте зробимо більше прикладів разом:
Памятайте, індексом сумації може бути будь-яка літера,
i та j є найбільш популярними.
В наступних прикладах будемо використовувати не тільки ці літери, але і l чи k.
Приклад
\begin{equation}
\begin{split}
\sum_{{k=2}}^{4}\sum_{{l=1}}^{2} (2\cdot k-l)=
\end{split}
\end{equation}
Рішення: рахуємо по кроках 1 і 2,
перше внутрішня сума:
\begin{equation}
\begin{split}
\sum_{{k=2}}^{4}\sum_{{l=1}}^{2} (2\cdot k-l)&=
\sum_{k=2} ^{4}(2\cdot k -1)+(2\cdot k-2)\\&=
\sum_{k=2} ^{4}(4\cdot k-3) \\Тепер \hspace{0.4em} зовнішня\hspace{0.4em}\\ сума\hspace{0.4em} як\hspace{0.4em}\\ завжди:
\\&=(4\cdot 2-3)+(4\cdot 3 -3)+
\\&+(4\cdot 4-3)
\\після\hspace{0.4em} додавання \\ \hspace{0.4em} отримаємо:
\\&=27
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\sum_{{k=2}}^{4}\sum_{{l=1}}^{2} (2\cdot k-l)\\&=
\sum_{k=2} ^{4}(2\cdot k -1)+(2\cdot k-2)\\&=
\sum_{k=2} ^{4}(4\cdot k-3)
\\&=(4\cdot 2-3)+(4\cdot 3 -3)+
\\&+(4\cdot 4-3)
\\&=27
\end{split}
\end{equation}
Тепер ваша черга.
Порахуйте приклади нижче,
рішення можете перевірити внизу.
Приклад 2 (для практики)
$ \sum_{k=3}^{5}\sum_{l=1}^{3} (k-2\cdot l)$
Приклад 3 (для практики)
$ \sum_{k=2}^{4}\sum_{l=2}^{4} (-k+l)$
Добуток у подвійній сумі
Давайте порахуємо разом:
Знайдіть подвійну суму $xy$
Спочатку внутрішню
суму підставляючи 1 та 2 в змінну y. Потім зовнішню суму,
де змінна тепер х як завжди:
\begin{equation}
\begin{split}
\sum_{{x=1}}^{2}\sum_{{y=1}}^{2} (x\cdot y)&=\sum_{{x=1}}^{2}(x\cdot 1)+(x\cdot 2)
\\&=(1\cdot 1 + 1\cdot 2) + (2\cdot 1 + 2\cdot 2)
\\&=1+2+2+4
\\&=9
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\sum_{{x=1}}^{2}\sum_{{y=1}}^{2} (x\cdot y)=\\&=\sum_{{x=1}}^{2}(x\cdot 1)+(x\cdot 2)
\\&=(1\cdot 1 + 1\cdot 2) +\\&+ (2\cdot 1 + 2\cdot 2)
\\&=1+2+2+4
\\&=9
\end{split}
\end{equation}
(також можна було зразу додати х+2х=3х та рахувати простіше)
Ще один приклад з діленням разом:
\begin{equation}
\begin{split}
\sum_{{i=5}}^{6}\sum_{{j=1}}^{2} \frac{j^2}{i}&=\sum_{{i=5}}^{6} \frac{1^2}{i}
+\frac{2^2}{i}
\\&=\Big(\frac{1^2}{5}+\frac{2^2}{5}\Big)
+\Big(\frac{1^2}{6}+\frac{2^2}{6}\Big)
\\&=\Big(\frac{1+4}{5}\Big)+\Big(\frac{1+4}{6}\Big)
\\&=1+\frac{5}{6}=\frac{11}{6}
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\sum_{{i=5}}^{6}\sum_{{j=1}}^{2} \frac{j^2}{i}=\\&=\sum_{{i=5}}^{6} \frac{1^2}{i}
+\frac{2^2}{i}
\\&=\Big(\frac{1^2}{5}+\frac{2^2}{5}\Big)
+\Big(\frac{1^2}{6}+\frac{2^2}{6}\Big)
\\&=\Big(\frac{1+4}{5}\Big)+\Big(\frac{1+4}{6}\Big)
\\&=1+\frac{5}{6}=\frac{11}{6}
\end{split}
\end{equation}
(можна було зразу додати $ \frac{1^2}{i}
+\frac{2^2}{i}=\frac{5}{i}$)
Ще один разом:
\begin{equation}
\begin{split}
\sum_{{i=7}}^{8}\sum_{{j=3}}^{4} \frac{j+1}{(i-1)^2}&=\sum_{{i=7}}^{8} \frac{3+1}{(i-1)^2}
+ \frac{4+1}{(i-1)^2}
\\&= \Big(\frac{3+1}{(7-1)^2}+ \frac{4+1}{(7-1)^2}\Big)+
\\&+\Big(\frac{3+1}{(8-1)^2}+ \frac{4+1}{(8-1)^2}\Big)
\\&=\Big(\frac{4}{36}+\frac{5}{36}\Big)
+\Big(\frac{4}{49}+\frac{5}{49}\Big)
\\&=\frac{3}{12}+\frac{9}{49}
\\&=\frac{255}{588}=\frac{85}{196}
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\sum_{{i=7}}^{8}\sum_{{j=3}}^{4} \frac{j+1}{(i-1)^2}=\\&=\sum_{{i=7}}^{8} \frac{3+1}{(i-1)^2}
+ \frac{4+1}{(i-1)^2}
\\&= \Big(\frac{3+1}{(7-1)^2}+ \frac{4+1}{(7-1)^2}\Big)+
\\&+\Big(\frac{3+1}{(8-1)^2}+ \frac{4+1}{(8-1)^2}\Big)
\\&=\Big(\frac{4}{36}+\frac{5}{36}\Big)
+\Big(\frac{4}{49}+\frac{5}{49}\Big)
\\&=\frac{3}{12}+\frac{9}{49}
\\&=\frac{255}{588}=\frac{85}{196}
\end{split}
\end{equation}
Гарний приклад з j в степені
i (також легкий
):
Порахуємо разом
:
\begin{equation}
\begin{split}
\sum_{{i=3}}^{4}\sum_{{j=1}}^{2} \frac{i^2}{1+j^i}&=
\sum_{{i=3}}^{4} \frac{i^2}{1+1^i}
+ \frac{i^2}{1+2^i}\\часта\hspace{0.4em}\\помилка:
\\& \color{red} {\neq \frac{3^2}{1+1^3}+\frac{4^2}{1+1^4}}\\
правильно\hspace{0.4em}підставити\hspace{0.4em}3\hspace{0.4em}в\hspace{0.4em}обидва\\
\hspace{0.4em}дроби\hspace{0.4em}та\hspace{0.4em}4\hspace{0.4em}в\hspace{0.4em}обидва:\\
\\&= \frac{\color{red}{3^2}}{1+1^\color{red}{3}}+
\frac{\color{red}{3^2}}{1+2^\color{red}{3}}+
\\&+\frac{\color{red}{4^2}}{1+1^\color{red}{4}}+
\frac{\color{red}{4^2}}{1+2^\color{red}{4}}
\\&=\frac{9}{2}+\frac{9}{9}+\frac{16}{2}+\frac{16}{17}
\\&=\frac{1377+306+2448+288}{306}
\\&=\frac{4419}{306}\\скоротимо\hspace{0.4em}
на\hspace{0.4em}9
\\&=\frac{491}{34}
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\sum_{{i=3}}^{4}\sum_{{j=1}}^{2} \frac{i^2}{1+j^i}\\&=
\sum_{{i=3}}^{4} \frac{i^2}{1+1^i}
+ \frac{i^2}{1+2^i}
\end{split}
\end{equation}
Common mistake:
\begin{equation}
\begin{split}
& \color{red} {\neq \frac{3^2}{1+1^3}+\frac{4^2}{1+1^4}}\\
\end{split}
\end{equation}
Plug in 3 and 4 in each of 2 fractions:
\begin{equation}
\begin{split}
\\&= \frac{\color{red}{3^2}}{1+1^\color{red}{3}}+
\frac{\color{red}{3^2}}{1+2^\color{red}{3}}+
\\&+\frac{\color{red}{4^2}}{1+1^\color{red}{4}}+
\frac{\color{red}{4^2}}{1+2^\color{red}{4}}
\\&=\frac{9}{2}+\frac{9}{9}+\frac{16}{2}+\frac{16}{17}
\\&=\frac{1377+306+2448+288}{306}
\\&=\frac{4419}{306}
\\&=\frac{491}{34}
\end{split}
\end{equation}
Тепер ваша черга практикуватися.
Перевірити рішення можете як завжди внизу.
Приклад 4 (практика)
$ \sum_{i=5}^{8}\sum_{j=3}^{5} j^3\cdot i^2$
Приклад 5 (практика)
$ \sum_{i=0}^{1}\sum_{j=1}^{2} j^2+ i^2$
Приклад 6 (практика)
$ \sum_{i=5}^{7}\sum_{j=10}^{12} \frac{j^2\cdot i}{2}$
Приклад 7 (практика)
$ \sum_{i=1}^{2}\sum_{j=1}^{3} \frac{j-i}{j}$
Приклад 8 (практика)
$ \sum_{i=1}^{2}\sum_{j=1}^{3}j^i$
Подвійна сума однієї змінної
Подивимося на подвійну суму з однією
змінною після двох знаків суми.
Приклад:
\begin{equation}
\begin{split}
\sum_{{i=1}}^{5}\sum_{{j=1}}^{4} j&
\end{split}
\end{equation}
Рішення: Вирішимо як і поперднi.
Cпочатку внутрішню суму з індексом j:
\begin{equation}
\begin{split}
\sum_{{i=1}}^{5}\sum_{{j=1}}^{4} j&=\sum_{{i=1}}^{5} (1+2+3+4)
\\&=\sum_{{i=1}}^{5} 10
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\sum_{{i=1}}^{5}\sum_{{j=1}}^{4} j=\\&=\sum_{{i=1}}^{5} (1+2+3+4)
\\&=\sum_{{i=1}}^{5} 10
\end{split}
\end{equation}
тепер маємо знак суми та константу
(нема літери 'i', все інше це константа).
Дальше ми додаємо константу 10 разів,
як ми знаємо з попередніх тем:
\begin{equation}
\begin{split}
\sum_{{i=1}}^{5}\sum_{{j=1}}^{4} j&=\sum_{{i=1}}^{5} (1+2+3+4)
\\&=\sum_{{i=1}}^{5} 10
\\&=\color{blue}{10 +10+10+10+10}
\\&=\color{blue}{50}
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\sum_{{i=1}}^{5}\sum_{{j=1}}^{4} j=\\&=\sum_{{i=1}}^{5} (1+2+3+4)
\\&=\sum_{{i=1}}^{5} 10
\\&=10 +10+10+10+10
\\&=50
\end{split}
\end{equation}
Порахуємо ще один, цього разу зі змінною "i"
Приклад:
\begin{equation}
\begin{split}
\sum_{{i=1}}^{5}\sum_{{j=1}}^{4} i^2&
\end{split}
\end{equation}
Рішення: Спочатку внутрішню суму. Індекс сумації
'j,' але його немає біля знаку суми, тільки константа $i^2$.
Тому ми додамо $i^2$
чотири рази (див.
Сума константи
)
Тому:
\begin{equation}
\begin{split}
\sum_{{i=1}}^{5}\sum_{{j=1}}^{4} i^2&=\sum_{{i=1}}^{5} 4\cdot i^2\\ \\
тепер \hspace{0.4em} вирішуємо\\\hspace{0.4em}як\hspace{0.4em}
завжди:
\\&=\sum_{{i=1}}^{5} 4\cdot 1^2 +4\cdot 2^2+
\\&+4\cdot 3^2+4\cdot 4^2+ 4\cdot 5^2
\\&=4\cdot (1+4+9+16+25)
\\&=4\cdot 55
\\&=220
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\sum_{{i=1}}^{5}\sum_{{j=1}}^{4} i^2=\\&=\sum_{{i=1}}^{5} 4\cdot i^2
\\&=\sum_{{i=1}}^{5} 4\cdot 1^2 +4\cdot 2^2+
\\&+4\cdot 3^2+4\cdot 4^2+ 4\cdot 5^2
\\&=4\cdot (1+4+9+16+25)
\\&=4\cdot 55
\\&=220
\end{split}
\end{equation}
Останній разом, дальше ви самі:
\begin{equation}
\begin{split}
\sum_{{i=5}}^{7}\sum_{{j=10}}^{15} i^{2\cdot i}
\end{split}
\end{equation}
Порахуємо внутрішню суму. Знову,
$i^{2\cdot i}$ є просто константою, тому що немає індексу сумації 'j'
. Скільки разів ми додаємо $i^{2\cdot i}$?
Стільки, скільки є чисел між 10 і 15 включно.
Тобто $15-10+1=6$ разів
(перевірте: 10, 11, 12, 13, 14, 15).
Отримаємо:
\begin{equation}
\begin{split}
\sum_{{i=5}}^{7}\sum_{{j=10}}^{15} i^{2\cdot i}&= \sum_{{i=5}}^{7} 6\cdot i^{2\cdot i}
\\i\hspace{0.4em}тепер\hspace{0.4em}як\hspace{0.4em}завжди
\\&=6\cdot 5^{2\cdot 5}+6\cdot 6^{2\cdot 6}+6\cdot 7^{2\cdot 7}
\\&=6\cdot( 5^{10}+6^{12}+7^{14})
\\&=4082457724860
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\sum_{{i=5}}^{7}\sum_{{j=10}}^{15} i^{2\cdot i}=\\&= \sum_{{i=5}}^{7} 6\cdot i^{2\cdot i}
\\&=6\cdot 5^{2\cdot 5}+6\cdot 6^{2\cdot 6}+6\cdot 7^{2\cdot 7}
\\&=6\cdot( 5^{10}+6^{12}+7^{14})
\\&=4082457724860
\end{split}
\end{equation}
Тепер ваша черга.
Якщо виникнуть проблеми перечитайте кроки 1 і 2, або перейдіть
по ссилкам та ознайомтесь з попередніми темами.
Приклад 9 (практика)
$ \sum_{i=8}^{9}\sum_{j=1}^{5} i$
Приклад 10 (практика)
$ \sum_{i=1}^{3}\sum_{j=15}^{20} (i-3)^2$
Приклад 11 (практика)
$ \sum_{i=10}^{12}\sum_{j=2}^{4} j^3$
Приклад 12 (практика)
$ \sum_{i=1}^{3}\sum_{j=30}^{32} i^i$
Що якщо немає жодного
з індексів сумації біля знаків суми?
Подвійна сума константи
Подивимося на наступну подвійну
суму без змінних "i" та "j":
Приклад:
\begin{equation}
\begin{split}
\sum_{{i=1}}^{5}\sum_{{j=1}}^{4} 5k&
\end{split}
\end{equation}
Рішення: тут ми маємо тільки сталу (константу) 5k.
Тому ми додамо 5к чотири рази: (тому що j йде від 1 до
4):
1. $\sum_{{i=1}}^{5}\sum_{{j=1}}^{4} 5k=\sum_{{i=1}}^{5}4\cdot 5k=\sum_{{i=1}}^{5}20k$
1. $\sum_{{i=1}}^{5}\sum_{{j=1}}^{4} 5k=\sum_{{i=1}}^{5}4\cdot 5k=
\\ =\sum_{{i=1}}^{5}20k$
2. тепер:
$\sum_{{i=1}}^{5}20 k=5\cdot 20k=100k$
Отримаємо:
$\sum_{{i=1}}^{5}\sum_{{j=1}}^{4} 5k=100k$
Сталою може бути будь-що, не тільки літери.
Вирішимо разом:
:
\begin{equation}
\begin{split}
\sum_{{i=1}}^{5}\sum_{{j=1}}^{6} 😃&
\end{split}
\end{equation}
Рішення: спочатку додамо емодзі 6х:
$\sum_{{i=1}}^{5}\sum_{{j=1}}^{6} 😃=\sum_{{i=1}}^{5}6\cdot 😃$
дальше 5х:
$\sum_{{i=1}}^{5}6\cdot 😃=5\cdot 6\cdot 😃=30\cdot 😃$
Все, що не містить індексу сумації є сталою.
Приклад 13 (практика)
$ \sum_{i=0}^{6}\sum_{j=3}^{8} p$
Приклад 14 (практика)
$ \sum_{i=1}^{6}\sum_{j=4}^{9} 1$
Приклад 15 (практика)
$ \sum_{i=7}^{10}\sum_{j=1}^{12} 🗼$
Рішення в кінці сторінки. Порахуйте самі та перевірте.
Рішення
1. 32
2. 0
3. 0
4. 37584
5. 12
6. 3285
7. 0.5
8. 20
9. 85
10. 30
11. 297
12. 96
13. 42p
14. 36
15. 48🗼